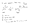It is an unfortunate reality that many people try to learn linear algebra with algebra when what’s going on is essentially a geometric matter (that means you can understand it with pictures). I previously described this point of view in Understanding Regression with Geometry and here I’m going to attempt something similar with the Singular Value Decomposition.
The Singular Value Decomposition is the ultimate linear algebra concept. With it you can understand, among many things, what a matrix really is, a variety of other related decompositions, eigenvalues and eigenvectors, and pseudo-inverses. On the computer science/data science side, the Singular Value Decomposition underlies techniques like Latent Semantic Analysis in NLP and is related to a variety of collaborative filtering/matrix factorization algorithms used in recommendation systems.
To get to the Singular Value Decomposition we’re first going to dispel the myth that a vector is a list of numbers and matrix is an array of them. Then we’ll present and describe the decomposition.
The background assumed here is that you know what a vector is (bonus if you think it is a list of numbers), and likewise a matrix. You should be familiar with:
- Vectors can be added: [1,2] + [3, 4] = [4, 6]
- A vector can be multiplied by a constant: 3[1,2] = [3,6]
- Vectors can be graphed by drawing an arrow pointing from the origin to the specified point.
- Matrices can be multiplied (slightly more complicated but we don’t actually need to do any actual matrix multiplication don’t worry).
Technical Note: this article is restricted to considering real numbers and finite dimensions (our vectors are made up of a finite list of numbers, instead of an infinite list). Also, we add the technical assumption that we have an inner product structure, which you can just take to mean that the Pythagorean Theorem works.¹ Everything we do will work with complex numbers or with infinite dimensions: the former requires adjusting a few words; the latter makes things extremely complicated.
A Vector is not a List of Numbers
For starters, let’s set up our geometric context: good old fashioned Euclidean space. You should picture either a perfectly flat infinite plane (2-dimensional space) or my personal favorite, 3 dimensional space like the one we live in.
Here’s the catch. You are probably used to drawing an x- and y-axis on the 2-dimensional space, or x-, y-, and z-axes on the 3-dimensional space. This is very misleading, so please erase them from your picture. Instead, place a dot somewhere in the space (the “middle” usually) and call it the origin.
Please note that everything we are going to do works in n dimensions, where n could be a large integer. I am a mere mortal and I can only visualize in 3 dimensions and I draw best in 2. If you can think in more of them, more power to you.
A Vector is a Vector is a Vector
The diagram below shows on the left two vectors A and B, as well as their sum. On the right are two different ways of adding axes to the 2-dimensional space. Depending on how we choose the axes, we get different numbers! We’re not going to worry about the relationship between those numbers (that is, of course, where the algebra comes in, and I promised we wouldn’t do any of that).
The essential point is that the vector is the vector is the vector: its existence is independent of the numbers used to describe it, if any. This is one of the essential insights underlying Einstein’s theories of relativity: depending on your perspective, you might describe something differently; but that can’t change what it is.

A few fine points here. First of all, what a vector is includes its length (distance from the origin) and its angles relative to other vectors.¹ That this is the essence of having a geometry. Second, we chose our axes to be orthogonal (perpendicular), something we didn’t have to do. But things get very complicated if you don’t choose them so and throughout this article we will always assume we have orthogonal axes.² Third, we should technically pick a basis and not axes. However, this just makes things more complicated by adding algebra and subtracting intuition. If you are concerned, the basis is just made by choosing the vector of length 1 pointing in the positive direction of each axis.³
A Vector Lives in a Vector Space
Not much to say here. A vector space is a fancy word for… the space that the vectors live in. In a sense, it is just the collection of all the relevant vectors. And there is a special vector 0 (the origin). So in the diagram above, the vectors lived in a 2 dimensional vector space.
The only reason I bring this up is because we will need to deal with more than one vector space at a time. For example, we might have a 2 dimensional vector space V and a 4 dimensional vector space W. The vectors in V have nothing to do with the vectors in W (for now). You can’t add a vector in V to a vector in W or anything.
A Matrix is not an Array of Numbers
“It is my experience that proofs involving matrices can be shortened by 50% if one throws the matrices out.” — Emil Artin
A lot of confusion here stems from the fact that, in a large number of computing contexts, a matrix is just an array of numbers and doesn’t participate in the full mathematical structure involved. But, if you are reading this, you are hopefully interested in that full mathematical structure.
A Matrix is a (Linear) Map between Vector Spaces
A “map” is just a function but with the connotation that it “preserves structure.” A function (in math) is something that takes in inputs and gives out outputs. In the context of a vector space, the structure is “there is an origin” and “you can add vectors” as well as “multiply them by a constant.” This structure is called linearity so in this context by “map” we always implicitly mean “linear map” (hence the name: linear algebra).
So a matrix is a function f that takes vectors from one vector space (“the source”) and returns vectors in another vector space (“the target”). Plus it has to satisfy three properties to make it linear:

In English:
In a 2 dimensional source vector space, we can pick two general vectors like A and B as shown and the function can return any output for those two inputs. In an n-dimensional source, we need to pick n general vectors. The target can be any number of dimensions from 0 to 1 trillion or higher. Note by “general” I’m ruling out a few degenerate situations like (say) if A and B are the same vector, or B is twice A.⁴ With this setup, we require:
- The function takes the origin to the origin
- The function applied to a sum f(A + B) is the same as the sum if we apply the function first: f(A) + f(B).
- Likewise with scalar multiples: f(cA) = c * f(A).
Note that, on occasion, the source and the target could be the same, but that doesn’t change anything conceptually.
Last thing about what a matrix is. Just like the numbers in a vector change when we re-assign our axes, so do the numbers in a matrix. They depend on the axes used in both the source and the target. So really, a matrix is a representation of a linear map with an implicit or explicit choice of the axes in the source and target spaces.
In the following, we will assume every matrix comes with an implicit choice of axes; if we change the axes, the numbers in the matrix will change but the linear map itself won’t. For this reason we will slightly abuse the term and use “matrix” to mean “linear map.” The essential insight here is that you shouldn’t think about arrays of numbers at all: you should think about linear maps.
What Linear Maps Do
Okay, so now let’s build up a stable of examples. The diagram below shows some possible things that a linear map between two 2-dimensional vector spaces can do. The images f(A) and f(B) in the target are just labeled A and B for simplicity.
Items 1–4 show some things that a linear map can do. In addition, it can do any combination of these things, and an example is shown in the bottom right.
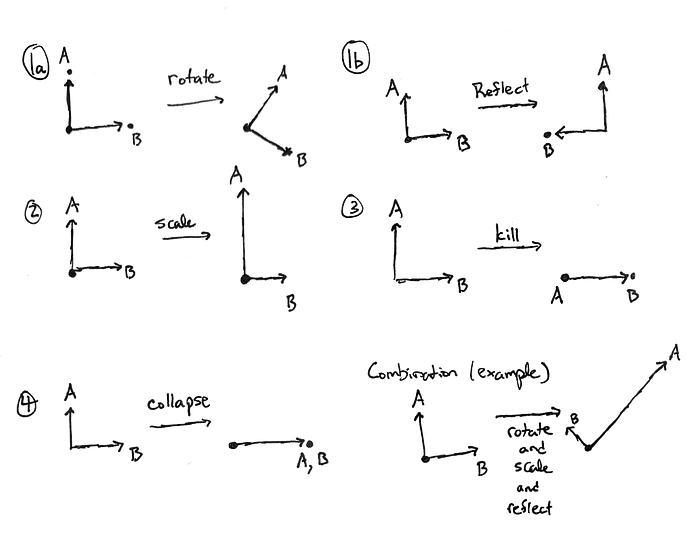
The crucial thing to keep in mind is that in an n-dimensional space, a lot more combinations of these make sense. For example, with 5 dimensions and perpendicular vectors A, B, C, D, and E, we might have A, B, and C subject to a three dimensional rotation along with a reflection of C, D collapsed onto C, and E killed. (Yes, really, it’s called “killing” the vector; a violent metaphor but that’s what mathematicians say). In some contexts, a lot more can happen in dimensions higher than 2 or 3, but this is not one of those contexts.
The Singular Value Decomposition
We are now in a position to give an informal statement of the Singular Value Decomposition.
Theorem (Singular Value Decomposition, Informal Statement). Every linear map is just a combination of rotation, reflection, scaling, and killing of vectors, provided the axes are chosen correctly.
A couple points. “Killing” a vector is really just scaling it by zero. Notice also that I left out collapsing: collapsing is actually made up of the others, as we will see.
So if you understand the diagram above (and how it would work in, say, 4 dimensions), then you understand the essence of everything there is to know about a linear map in this context (officially: real, finite dimensional vector spaces with an inner product structure).
Here’s an example. If you look at the diagram above, you won’t see anything like a “smush.” In fact, the “smush” shown is really a scaling of a single vector; but instead of thinking about A and B, we need to consider the vectors x and y shown.
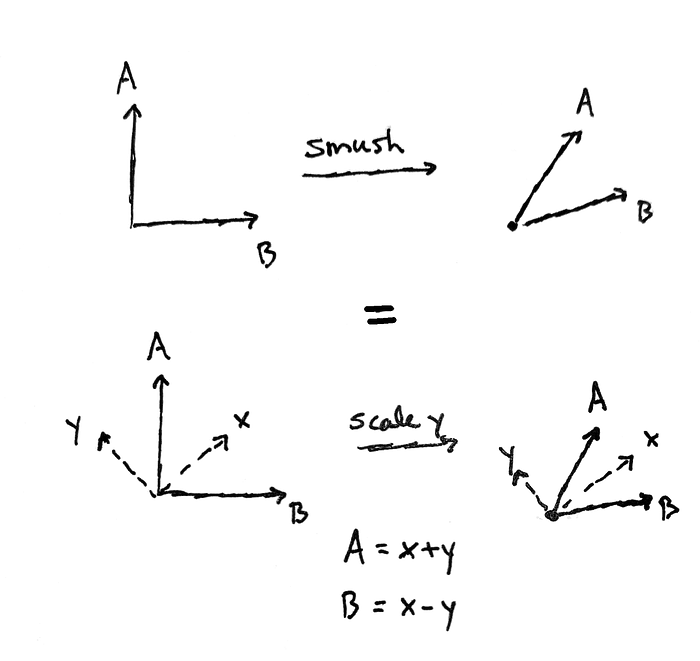
Remember, we said that to describe a linear map from a 2-dimensional source vector space, we just need to pick two generic vectors and see where they go. But the point is that, if those two vectors are chosen carefully, the map will admit a simple description.
Now, I said that we should pick the axes carefully, not these two vectors. But really doing one is doing the other. I have suggestively named the two vectors x and y because really, we are picking x- and y-axes, and then making x and y just vectors that point along those axes. Previously we had chosen A and B to point out our axes for us (the A-axis goes along A, the B-axis goes along B – we can name the axes whatever we want). So thinking about the two vectors is the same as thinking about the two axes. Do whichever comes naturally to you.
Official Statement
The official statement of the Singular Value Decomposition necessarily involves just the slightest amount of Algebra, but I’ll endeavor to explain it geometrically in English.
Theorem (Singular Value Decomposition).
Let A be a matrix with m rows and n columns (m⨉n), regarded as a linear map from an n-dimensional vector space V to an m-dimensional vector space W.
Then A may be factored as the product of three matrices A = R*D*S, where:
- S is an n⨉n rotation matrix with source and target both V
- D is m⨉n diagonal matrix with source V and target W: its only non-zero entries are on the diagonal. For example:

- R is an m⨉m rotation matrix with source W and target W.
Recall that the linear map A implicitly comes with a choice of axes, specifically the usual x-, y-, z-, etc.-axes in both V and W.
This means that the linear map A from V to W may be considered to happen in three steps. First, rotate vectors in V using S. Second, scale vectors along each axis by a constant (possibly 0 which kills them or also negative) and then put them into W by using the axes that implicitly come with A (using D). Finally, perform a rotation of the vectors in W (using R).
Please note that the way matrix multiplication works, S acts first, then D, then R (since the vector goes on the right).
Please also note that if you look up the Singular Value Decomposition on Wikipedia you will see a slightly different statement. My version is, I assure you, also true and much simpler to boot.
The statement on Wikipedia uses a “transpose” of S instead of S itself. This is to make explicit that the rotation matrices are effectively rejiggering the axes that we chose. The Wikipedia statement also allows S and R to include an extra reflection if they want, but we can accomplish that with a negative scaling in D instead.
But, once we realize that a rotation matrix is equivalent to changing the axes (it is, I promise), then hopefully you will see why the informal statement of theorem above is true. If we were allowed to choose our axes appropriately in the first place, we could just write A as a single diagonal matrix which just scales the axes and moves them from the source V to the target W.
Some terminology: the special axes that make A diagonal in the source and target are called left-singular vectors (in the target) and right-singular vectors (in the source). They are the columns of R and rows S are the left- and right-singular vectors. The values on the diagonal of D are called the singular values.
Partial Proof Sketch
I’m only going to provide a construction of the matrices S, R, and D to add a little more geometric intuition to the Singular Value decomposition. This won’t amount to a full proof.
The Spectral Theorem
The Singular Value Decomposition generalizes the Spectral Theorem. The spectral theorem is so-called because the idea is that there is a ghost (“specter”) of the “true nature” of the matrix that can be extracted. In the context of the Spectral Theorem, the “true nature” is that we can choose axes (using the singular vectors) so that the matrix is just a scaling matrix. “Eigen” is the German word for “true” and so in the context of the Spectral Theorem, the singular vectors are instead called “eigenvectors” and the singular values are instead called “eigenvalues.”
The Spectral Theorem is only for square matrices which have the same source and target. It also only works for some square matrices (“normal” ones), not all. By comparison, the Singular Value Decomposition works for non-square matrices and it works for every matrix.
The Matrix Transpose
You may have heard of the matrix transpose. Provided we have been nice and not naughty when choosing our axes (they need to be perpendicular), the matrix transpose is just flipping a matrix across the diagonal and onto its side.

The transposes is a backwards map. If A maps the source V to the target W, then its transpose is backwards: the transpose instead has source W and target V.
Getting the Singular Values
Let A be a matrix with source V and target W. Following it by its transpose results in a map from the source to itself.

It turns out that the spectral theorem applies to this map. The eigenvectors provide the right-singular vectors. Likewise, if you first do A-transpose and then do A, you will get the left-singular vectors. Once you have these, all you have to do is extract the singular values as the square root of the eigenvalues. Proving that this will work is a little bit more complicated, but not crazy.
Conclusion
I hope you have seen that treating a matrix as a linear map instead of an array of numbers is a very powerful means of understanding them. Each linear map can be described very simply as a diagonal scaling matrix provided the right set of axes is chosen for the source and target spaces. In applications, it is often those axes that are of interest as they in some sense provide the “true” and otherwise “latent” way of looking at the matrix.
As an exercise, if you’ve understood this you should be able to understand the Moore-Penrose Pseudoinverse which generalizes the inverse matrix to non-square matrices and non-invertible matrices.
References / Further Reading
If you followed this, you should be able to take this understanding to any good linear algebra textbook. What we called “axes” becomes a “basis” and most of the work of linear algebra comes from doing computations about bases as well as examining in greater detail and with more terminology what a matrix can do. But the vast majority can be understood through the lens of the Singular Value Decomposition.
[1] Officially, we are working with real finite-dimensional Hilbert Spaces, and the theorem has an appropriate generalization to any Hilbert space. As stated, to keep things simple, this article will always assume we are working in a finite-dimensional real vector space with an inner product-structure (which automatically makes it a Hilbert Space since we have finite dimension).
[2] In particular, if the axes aren’t orthogonal the transpose of a matrix will no longer consist of flipping the numbers over the diagonal.
[3] For those in the know, we are assuming we have an orthonormal basis but we’ll avoid talking about bases as much as possible.
[4] Officially, we require that the source vectors chosen be linearly independent and span the space, which makes them a basis. The official definition of “general” is loosely borrowed from the concept of generic in algebraic geometry and roughly means that, in the space of choices of basis vectors we use to define the linear map, the unacceptable choices form a sub-variety of co-dimension at least 1.
Source: https://towardsdatascience.com/the-singular-value-decomposition-without-algebra-ae10147aab4c