Machine Learning or ML is one of the most successful applications of Artificial intelligence which provides systems with automated learning without being constantly programmed. It has acquired a ton of noticeable quality lately due to its capacity to be applied across scores of ventures to tackle complex issues quickly and effectively. From Digital assistants that play your music to the products being recommended based on prior search, Machine Learning has taken over many aspects of our life. It is a skill in high demand as companies require software that can grasp data and provide accurate results. The core objective is to obtain optimal functions with less confusion.
1. WHAT IS MACHINE LEARNING?
Machine Learning is a segment that comes under Artificial Intelligence (AI) that increases the quality of applications by using previously assimilated data. It programs systems to learn and grasp data without having to feed a new code for every new similar activity. The aim is for the flow to be automated rather than continuously modified. Hence by experience and past intel, it improves the program by itself.
2. WHY MACHINE LEARNING?
The domain of Machine Learning is a continuously evolving field with high demand. Without human intervention, it delivers real-time results using the already existing and processed data. It generally helps analyze and assess large amounts of data with ease by developing data-driven models. As of today, Machine Learning has become a fast and efficient way for firms to build models and strategize plans.
3. ADVANTAGES OF MACHINE LEARNING
Completely Automated ( Zero human intervention)
Analyses large amounts of data
More efficient than traditional data analytical methods
Identifies trends and patterns with ease
Reliable and efficient
Less usage of workforce
Handles a variety of data
Accommodates for most forms of applications
4. COMMONLY USED ALGORITHMS IN MACHINE LEARNING
There are many different models in Machine Learning. Here are the most commonly used algorithms in the world today:
Machine Learning or ML is slowly but steadily having a huge impact on data-driven business decisions across the globe. It has also helped organizations with the correct intel to make more informed, data-driven choices that are quicker than conventional methodologies. Yet, there are many issues in Machine Learning that cannot be overlooked in spite of its high productivity.
5. LIST OF COMMON PRACTICAL ISSUES IN MACHINE LEARNING
1) LACK OF QUALITY DATA
One of the main issues in Machine Learning is the absence of good data. While upgrading, algorithms tend to make developers exhaust most of their time on artificial intelligence. Data quality is fundamental for the algorithms to work as proposed. Incomplete data, unclean data, and noisy data are the quintessential foes of ideal ML. Different reasons for low data quality are-
Data can be noisy which will result in inaccurate predictions. This often leads to less accuracy in classification and low-quality results. It is noted as one of the most common errors faced in terms of data.
Incorrect or incomplete information can also lead to faulty programming through Machine Learning. Having less information will lead the program to analyze based on the minimal data present. Hence, decreasing the accuracy of the results.
For better future actions, the generalizing of input and output of past data is crucial. But a common issue that occurs is, the output data can become difficult to generalize.
2) FAULT IN CREDIT CARD FRAUD DETECTION
Although this AI-driven software helps to successfully detect credit card fraud, there are issues in Machine Learning that make the process redundant. It is tough for the system to spot anything without adequate amounts of data, hence making them blind to any illegal connections. Hence detecting fraud without possessing a significant amount of data is close to impossible.
3) GETTING BAD RECOMMENDATIONS
Proposal engines are quite regular today. While some might be dependable, others may not appear to provide the necessary results. Machine Learning algorithms tend to only impose what these proposal engines have suggested. So if there is any modification in the necessity of the result, then the recommendation will be of no use. Creating a complex algorithm, collecting large amounts of data, and implementing the algorithm, leading to nothing but incorrect results in case of changed priorities is one of the biggest issues with Machine Learning
4) TALENT DEFICIT
Albeit numerous individuals are pulled into the ML business, however, there are still not many experts who can take complete control of this innovation. It is quite rare to find a trained professional who is capable of comprehending the problems in Machine Learning and be able to reach out to a reliable software solution for the same.
5) IMPLEMENTATION
Organizations regularly have examination engines working with them when they decide to move up to ML. The usage of fresher ML strategies with existing procedures is a complicated errand. Keeping up legitimate documentation and interpretation need to go a long way to facilitating maximum usage. There are issues in Machine Learning when it comes to implementation-
Slow deployment – Although the models of Machine Learning are time efficient the creating process of the same is quite the opposite. As it is still a young innovation the implementation time is slow.
Data Security – Saving confidential data on ML servers is a risk as the model will not be able to differentiate between sensitive and insensitive data.
Lack of data is another key issue faced during the implementation of the model. Without adequate data, it is not possible to give out valuable intel.
6) MAKING THE WRONG ASSUMPTIONS
ML models can’t manage datasets containing missing data points. Thus, highlights that contain a huge part of missing data should be erased. On the other hand, if there are a couple of missing qualities in an element, rather than erasing it, we could fill those vacant cells. The most ideal approach to manage these issues in Machine Learning is to ensure that your data doesn’t accompany gaping holes and can convey a considerable measure of presumptions.
7) DEFICIENT INFRASTRUCTURE
ML requires a tremendous amount of data stirring abilities. Inheritance frameworks can’t deal with the responsibility and clasp under tension. You should check if your infrastructure can deal with issues in Machine Learning. If it can’t, you should hope to upgrade it completely with good hardware and adaptable storage.
8) HAVING ALGORITHMS BECOME OBSOLETE WHEN DATA GROWS
ML algorithms will consistently require a lot of data when being trained. Frequently, these ML algorithms will be trained over a specific data index and afterward used to foresee future data, a cycle which you can only expect with a significant amount of effort. The earlier “accurate” model over the data set may presently not be considered accurate, at a point where the arrangement of data changes.
9) ABSENCE OF SKILLED RESOURCES
The other issues in Machine Learning are that deep analytics and ML in their present structures are still new technologies. From the start code to the maintenance and monitoring of the process, Machine Learning experts are required to maintain the process. Artificial Intelligence and Machine Learning industries are still freshers to the market. Finding enough resources in the form of manpower is also difficult. Hence, there is a lack of talented representatives available to develop and manage scientific substances for ML. Data researchers regularly need a mix of space insight just as top to bottom knowledge of mathematics, technology, and science.
10) CUSTOMER SEGMENTATION
Let us consider the data of human behavior by a user during a time for testing and the relevant previous practices. All things considered, an algorithm is necessary to recognize those customers that will change over to the paid form of a product and those that won’t. A model with this choice issue would permit a program to trigger relevant recommendations for the user based on his catalog’s behavior.
The lists of supervised learning algorithms in ML are:
Neural Networks
Naive Bayesian Model
Classification
Support Vector Machines
Regression
Random Forest Model
11) COMPLEXITY
Although Machine Learning and Artificial Intelligence are booming, a majority of these sectors are still in their experimental phases, actively undergoing a trial and error method. From the setting up of the system to instilling complex data and even coding, the procedure is extremely complicated and quite tedious. It is a time-consuming and strenuous procedure that cannot accommodate any kinds of errors or mistakes.
12) SLOW RESULTS
Another one of the most common issues in Machine Learning is the slow-moving program. The Machine Learning Models are highly efficient bearing accurate results but the said results take time to be produced. Due to an overload of data and requirements, it takes longer than expected to provide results. This is mainly because of the complex algorithm that they work on and the time it takes to derive usable results. Another reason is that it requires constant monitoring at every step of the process.
13) MAINTENANCE
Requisite results for different actions are bound to change and hence the data needed for the same is different. This needs editing the code and more resources for monitoring the changes as well. As the outputs need to be generalized, regular monitoring and maintenance are necessary. Consistent maintenance is the key to keep the program up to date
14) CONCEPT DRIFT
This occurs when the target variable changes, resulting in the delivered results being inaccurate. This forces the decay of the models as changes cannot be easily accustomed to or upgraded. To eradicate this problem, a model that can adapt to a whole array of changes is necessary.
15) DATA BIAS
This occurs when certain aspects of a data set need more importance than others. Focusing on particular features within the database in order to generalize the outcomes is very common in Machine Learning Models. This leads to inaccurate results, low outcome levels, and other such errors.
16) HIGH CHANCES OF ERROR
Many algorithms will contain biased programming which will lead to biased datasets. It will not deliver the right output and produces irrelevant information. The usage of this can lead to bigger errors in the business models. This commonly occurs when the planning process is not done right. As you must have figured out by now, Machine Learning is all about concise algorithms. Before creating the model it is imperative that they identify the accurate problem statement and create a strategy. The major issues that arise in Machine Learning are from the errors in planning before the implementation.
17) LACK OF EXPLAINABILITY
Machine Learning is often termed a “Black box” as deciphering the outcomes from an algorithm is often complex and sometimes useless. This basically means the outputs cannot be easily comprehended as it is programmed in specific ways to deliver for certain conditions. This lack of explainability will make the reverse engineering of an algorithm nearly impossible, reducing the credibility of the algorithm.
CONCLUSION
Although there are many issues in Machine Learning, Today it is noted as one of the most evolving industries with advanced technological developments. Many of the biggest companies use Machine Learning to assist with large-grouped data analytics. From medical diagnosis and its developments to prediction and classification, ML has become an important and highly used process.
Convolutional Neural Networks (CNNs) are neural networks that automatically extract useful features (without manual hand-tuning) from data-points like images to solve some given task like image classification or object detection.
Thebinomial distribution is a discrete probability distribution. It describes the outcome ofn independent trials in an experiment. Each trial is assumed to have only two outcomes, either success or failure. If the probability of a successful trial isp, then the probability of havingx successful outcomes in an experiment ofnindependent trials is as follows.
Problem
Suppose there are twelve multiple choice questions in an English class quiz. Each question has five possible answers, and only one of them is correct. Find the probability of having four or less correct answers if a student attempts to answer every question at random.
Solution
Since only one out of five possible answers is correct, the probability of answering a question correctly by random is 1/5=0.2. We can find the probability of having exactly 4 correct answers by random attempts as follows.
> dbinom(4, size=12, prob=0.2) [1] 0.1329
To find the probability of having four or less correct answers by random attempts, we apply the function dbinom with x = 0,…,4.
It is an unfortunate reality that many people try to learn linear algebra with algebra when what’s going on is essentially a geometric matter (that means you can understand it with pictures). I previously described this point of view inUnderstanding Regression with Geometryand here I’m going to attempt something similar with the Singular Value Decomposition.
The Singular Value Decomposition is the ultimate linear algebra concept. With it you can understand, among many things, what a matrix really is, a variety of other related decompositions, eigenvalues and eigenvectors, and pseudo-inverses. On the computer science/data science side, the Singular Value Decomposition underlies techniques like Latent Semantic Analysis in NLP and is related to a variety of collaborative filtering/matrix factorization algorithms used in recommendation systems.
To get to the Singular Value Decomposition we’re first going to dispel the myth that a vector is a list of numbers and matrix is an array of them. Then we’ll present and describe the decomposition.
The background assumed here is that you know what a vector is (bonus if you think it is a list of numbers), and likewise a matrix. You should be familiar with:
Vectors can be added: [1,2] + [3, 4] = [4, 6]
A vector can be multiplied by a constant: 3[1,2] = [3,6]
Vectors can be graphed by drawing an arrow pointing from the origin to the specified point.
Matrices can be multiplied (slightly more complicated but we don’t actually need to do any actual matrix multiplication don’t worry).
Technical Note: this article is restricted to considering real numbers and finite dimensions (our vectors are made up of a finite list of numbers, instead of an infinite list). Also, we add the technical assumption that we have an inner product structure, which you can just take to mean that the Pythagorean Theorem works.¹ Everything we do will work with complex numbers or with infinite dimensions: the former requires adjusting a few words; the latter makes things extremely complicated.
A Vector is not a List of Numbers
For starters, let’s set up our geometric context: good old fashioned Euclidean space. You should picture either a perfectly flat infinite plane (2-dimensional space) or my personal favorite, 3 dimensional space like the one we live in.
Here’s the catch. You are probably used to drawing an x- and y-axis on the 2-dimensional space, or x-, y-, and z-axes on the 3-dimensional space. This is very misleading, so please erase them from your picture. Instead, place a dot somewhere in the space (the “middle” usually) and call it the origin.
Please note that everything we are going to do works in n dimensions, where n could be a large integer. I am a mere mortal and I can only visualize in 3 dimensions and I draw best in 2. If you can think in more of them, more power to you.
A Vector is a Vector is a Vector
The diagram below shows on the left two vectors A and B, as well as their sum. On the right are two different ways of adding axes to the 2-dimensional space. Depending on how we choose the axes, we get different numbers! We’re not going to worry about the relationship between those numbers (that is, of course, where the algebra comes in, and I promised we wouldn’t do any of that).
The essential point is that the vector is the vector is the vector: its existence is independent of the numbers used to describe it, if any. This is one of the essential insights underlying Einstein’s theories of relativity: depending on your perspective, you might describe something differently; but that can’t change what it is.
A few fine points here. First of all, what a vector is includes its length (distance from the origin) and its angles relative to other vectors.¹ That this is the essence of having a geometry. Second, we chose our axes to be orthogonal (perpendicular), something we didn’t have to do. But things get very complicated if you don’t choose them so and throughout this article we will always assume we have orthogonal axes.² Third, we should technically pick a basis and not axes. However, this just makes things more complicated by adding algebra and subtracting intuition. If you are concerned, the basis is just made by choosing the vector of length 1 pointing in the positive direction of each axis.³
A Vector Lives in a Vector Space
Not much to say here. A vector space is a fancy word for… the space that the vectors live in. In a sense, it is just the collection of all the relevant vectors. And there is a special vector 0 (the origin). So in the diagram above, the vectors lived in a 2 dimensional vector space.
The only reason I bring this up is because we will need to deal with more than one vector space at a time. For example, we might have a 2 dimensional vector space V and a 4 dimensional vector space W. The vectors in V have nothing to do with the vectors in W (for now). You can’t add a vector in V to a vector in W or anything.
A Matrix is not an Array of Numbers
“It is my experience that proofs involving matrices can be shortened by 50% if one throws the matrices out.” — Emil Artin
A lot of confusion here stems from the fact that, in a large number of computing contexts, a matrix is just an array of numbers and doesn’t participate in the full mathematical structure involved. But, if you are reading this, you are hopefully interested in that full mathematical structure.
A Matrix is a (Linear) Map between Vector Spaces
A “map” is just a function but with the connotation that it “preserves structure.” A function (in math) is something that takes in inputs and gives out outputs. In the context of a vector space, the structure is “there is an origin” and “you can add vectors” as well as “multiply them by a constant.” This structure is called linearity so in this context by “map” we always implicitly mean “linear map” (hence the name: linear algebra).
So a matrix is a function f that takes vectors from one vector space (“the source”) and returns vectors in another vector space (“the target”). Plus it has to satisfy three properties to make it linear:
A Linear Map Satisfies Three Properties
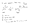
In English:
In a 2 dimensional source vector space, we can pick two general vectors like A and B as shown and the function can return any output for those two inputs. In an n-dimensional source, we need to pick n general vectors. The target can be any number of dimensions from 0 to 1 trillion or higher. Note by “general” I’m ruling out a few degenerate situations like (say) if A and B are the same vector, or B is twice A.⁴ With this setup, we require:
The function takes the origin to the origin
The function applied to a sum f(A + B) is the same as the sum if we apply the function first: f(A) + f(B).
Likewise with scalar multiples: f(cA) = c * f(A).
Note that, on occasion, the source and the target could be the same, but that doesn’t change anything conceptually.
Last thing about what a matrix is. Just like the numbers in a vector change when we re-assign our axes, so do the numbers in a matrix. They depend on the axes used in both the source and the target. So really, a matrix is a representation of a linear map with an implicit or explicit choice of the axes in the source and target spaces.
In the following, we will assume every matrix comes with an implicit choice of axes; if we change the axes, the numbers in the matrix will change but the linear map itself won’t. For this reason we will slightly abuse the term and use “matrix” to mean “linear map.” The essential insight here is that you shouldn’t think about arrays of numbers at all: you should think about linear maps.
What Linear Maps Do
Okay, so now let’s build up a stable of examples. The diagram below shows some possible things that a linear map between two 2-dimensional vector spaces can do. The images f(A) and f(B) in the target are just labeled A and B for simplicity.
Items 1–4 show some things that a linear map can do. In addition, it can do any combination of these things, and an example is shown in the bottom right.
Things a Linear Map Can Do.
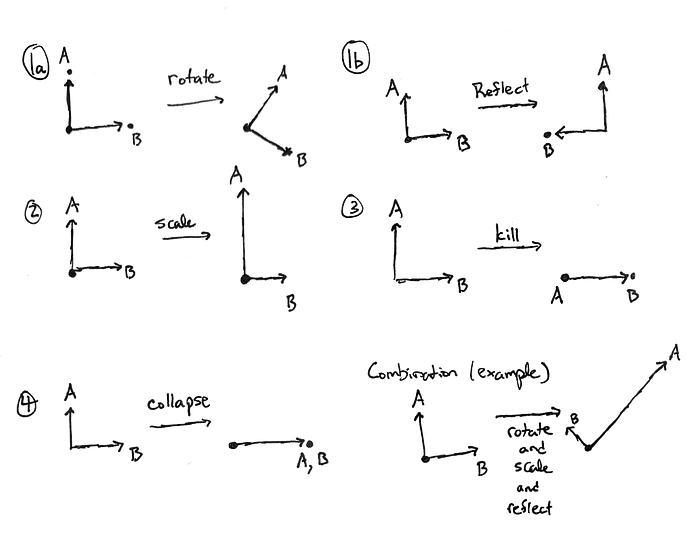
The crucial thing to keep in mind is that in an n-dimensional space, a lot more combinations of these make sense. For example, with 5 dimensions and perpendicular vectors A, B, C, D, and E, we might have A, B, and C subject to a three dimensional rotation along with a reflection of C, D collapsed onto C, and E killed. (Yes, really, it’s called “killing” the vector; a violent metaphor but that’s what mathematicians say). In some contexts, a lot more can happen in dimensions higher than 2 or 3, but this is not one of those contexts.
The Singular Value Decomposition
We are now in a position to give an informal statement of the Singular Value Decomposition.
Theorem (Singular Value Decomposition, Informal Statement). Every linear map is just a combination of rotation, reflection, scaling, and killing of vectors, provided the axes are chosen correctly.
A couple points. “Killing” a vector is really just scaling it by zero. Notice also that I left out collapsing: collapsing is actually made up of the others, as we will see.
So if you understand the diagram above (and how it would work in, say, 4 dimensions), then you understand the essence of everything there is to know about a linear map in this context (officially: real, finite dimensional vector spaces with an inner product structure).
Here’s an example. If you look at the diagram above, you won’t see anything like a “smush.” In fact, the “smush” shown is really a scaling of a single vector; but instead of thinking about A and B, we need to consider the vectors x and y shown.
Viewed Correctly, “Smushing” is a scaling of a single vector
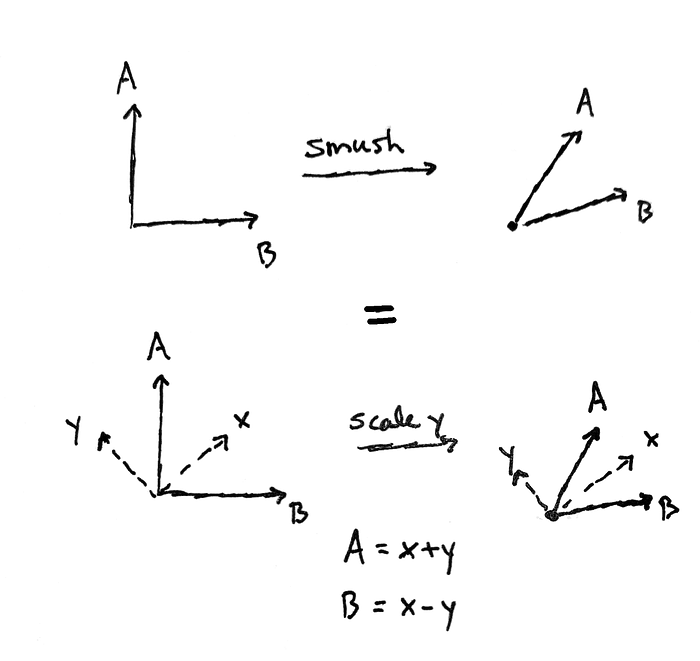
Remember, we said that to describe a linear map from a 2-dimensional source vector space, we just need to pick two generic vectors and see where they go. But the point is that, if those two vectors are chosen carefully, the map will admit a simple description.
Now, I said that we should pick the axes carefully, not these two vectors. But really doing one is doing the other. I have suggestively named the two vectors x and y because really, we are picking x- and y-axes, and then making x and y just vectors that point along those axes. Previously we had chosen A and B to point out our axes for us (the A-axis goes along A, the B-axis goes along B – we can name the axes whatever we want). So thinking about the two vectors is the same as thinking about the two axes. Do whichever comes naturally to you.
Official Statement
The official statement of the Singular Value Decomposition necessarily involves just the slightest amount of Algebra, but I’ll endeavor to explain it geometrically in English.
Theorem (Singular Value Decomposition).
Let A be a matrix with m rows and n columns (m⨉n), regarded as a linear map from an n-dimensional vector space V to an m-dimensional vector space W.
Then A may be factored as the product of three matrices A = R*D*S, where:
S is an n⨉n rotation matrix with source and target both V
D is m⨉n diagonal matrix with source V and target W: its only non-zero entries are on the diagonal. For example:
A non-square diagonal matrix with 1, 2.3, -7, and 0 on the diagonal
R is an m⨉m rotation matrix with source W and target W.
Recall that the linear map A implicitly comes with a choice of axes, specifically the usual x-, y-, z-, etc.-axes in both V and W.
This means that the linear map A from V to W may be considered to happen in three steps. First, rotate vectors in V using S. Second, scale vectors along each axis by a constant (possibly 0 which kills them or also negative) and then put them into W by using the axes that implicitly come with A (using D). Finally, perform a rotation of the vectors in W (using R).
Please note that the way matrix multiplication works, S acts first, then D, then R (since the vector goes on the right).
Please also note that if you look up the Singular Value Decomposition on Wikipedia you will see a slightly different statement. My version is, I assure you, also true and much simpler to boot.
The statement on Wikipedia uses a “transpose” of S instead of S itself. This is to make explicit that the rotation matrices are effectively rejiggering the axes that we chose. The Wikipedia statement also allows S and R to include an extra reflection if they want, but we can accomplish that with a negative scaling in D instead.
But, once we realize that a rotation matrix is equivalent to changing the axes (it is, I promise), then hopefully you will see why the informal statement of theorem above is true. If we were allowed to choose our axes appropriately in the first place, we could just write A as a single diagonal matrix which just scales the axes and moves them from the source V to the target W.
Some terminology: the special axes that make A diagonal in the source and target are called left-singular vectors (in the target) and right-singular vectors (in the source). They are the columns of R and rows S are the left- and right-singular vectors. The values on the diagonal of D are called the singular values.
Partial Proof Sketch
I’m only going to provide a construction of the matrices S, R, and D to add a little more geometric intuition to the Singular Value decomposition. This won’t amount to a full proof.
The Spectral Theorem
The Singular Value Decomposition generalizes the Spectral Theorem. The spectral theorem is so-called because the idea is that there is a ghost (“specter”) of the “true nature” of the matrix that can be extracted. In the context of the Spectral Theorem, the “true nature” is that we can choose axes (using the singular vectors) so that the matrix is just a scaling matrix. “Eigen” is the German word for “true” and so in the context of the Spectral Theorem, the singular vectors are instead called “eigenvectors” and the singular values are instead called “eigenvalues.”
The Spectral Theorem is only for square matrices which have the same source and target. It also only works for some square matrices (“normal” ones), not all. By comparison, the Singular Value Decomposition works for non-square matrices and it works for every matrix.
The Matrix Transpose
You may have heard of the matrix transpose. Provided we have been nice and not naughty when choosing our axes (they need to be perpendicular), the matrix transpose is just flipping a matrix across the diagonal and onto its side.
The Transpose Flips a Matrix and Puts it on its side
The transposes is a backwards map. If A maps the source V to the target W, then its transpose is backwards: the transpose instead has source W and target V.
Getting the Singular Values
Let A be a matrix with source V and target W. Following it by its transpose results in a map from the source to itself.
Following a map by its transpose results in a map from the source back to itself
It turns out that the spectral theorem applies to this map. The eigenvectors provide the right-singular vectors. Likewise, if you first do A-transpose and then do A, you will get the left-singular vectors. Once you have these, all you have to do is extract the singular values as the square root of the eigenvalues. Proving that this will work is a little bit more complicated, but not crazy.
Conclusion
I hope you have seen that treating a matrix as a linear map instead of an array of numbers is a very powerful means of understanding them. Each linear map can be described very simply as a diagonal scaling matrix provided the right set of axes is chosen for the source and target spaces. In applications, it is often those axes that are of interest as they in some sense provide the “true” and otherwise “latent” way of looking at the matrix.
As an exercise, if you’ve understood this you should be able to understand the Moore-Penrose Pseudoinverse which generalizes the inverse matrix to non-square matrices and non-invertible matrices.
References / Further Reading
If you followed this, you should be able to take this understanding to any good linear algebra textbook. What we called “axes” becomes a “basis” and most of the work of linear algebra comes from doing computations about bases as well as examining in greater detail and with more terminology what a matrix can do. But the vast majority can be understood through the lens of the Singular Value Decomposition.
[1] Officially, we are working with real finite-dimensional Hilbert Spaces, and the theorem has an appropriate generalization to any Hilbert space. As stated, to keep things simple, this article will always assume we are working in a finite-dimensional real vector space with an inner product-structure (which automatically makes it a Hilbert Space since we have finite dimension).
[2] In particular, if the axes aren’t orthogonal the transpose of a matrix will no longer consist of flipping the numbers over the diagonal.
[3] For those in the know, we are assuming we have an orthonormal basis but we’ll avoid talking about bases as much as possible.
[4] Officially, we require that the source vectors chosen be linearly independent and span the space, which makes them a basis. The official definition of “general” is loosely borrowed from the concept of generic in algebraic geometry and roughly means that, in the space of choices of basis vectors we use to define the linear map, the unacceptable choices form a sub-variety of co-dimension at least 1.
